Education and Early Childhood Learning

SolveMe Mobiles

Introduce algebraic concepts using puzzles on vertical surfaces.

---

A Grade 4/5 teacher used the model of thinking classrooms regularly with her learners. Thinking classroom practices are based on Peter Liljedahl’s research and are designed to create learner-centred, learner-driven mathematical thinking and learning as students observe, compare, and discuss how to approach a problem-solving task and record their thinking.

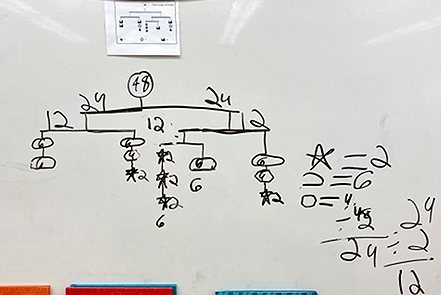
For this lesson, the teacher introduced algebraic concepts. She used SolveMe mobiles to drive the questions for the lesson, which were an engaging way to introduce the concepts of algebra with visual puzzles. The intent was to share with groups of learners a series of SolveMe mobiles that got progressively more difficult, thereby requiring more and more algebraic thinking from learners.

To start the lesson, learners all chose a playing card as they moved into their visibly random groupings of three, each located at vertical, non-permanent surfaces that were spread out around the room. Most groups worked on the classroom whiteboards, while two groups worked on glass window surfaces and one group worked on a shower curtain that was hung on the wall. Before assigning the first puzzle to the groups, the teacher led a discussion reviewing the classroom protocols that helped enhance communication and collaboration, and ensured all voices were heard and valued in the groups. In this classroom, there was no “official front” of the room, and the teacher regularly addressed the class from a variety of locations. From their groups, many of the learners offered their thoughts and referred to the anchor charts supporting these topics posted in the room.

The teacher then described the first task orally and asked the learners to turn over their SolveMe mobile puzzle, which was posted on their vertical surface (the teacher had printed off a succession of SolveMe mobile problems for the learners to post on their vertical surfaces as they moved through the tasks). They were encouraged to solve their problem using representations and strategies that made sense to them, and to document their thinking as a group. Learners approached the puzzles in unique ways and engaged in the learning process, working at their level of development. The focus of the task was on the process rather than the answers, as they drew on multiple ways of thinking and building on each other’s ideas. Each group shared one whiteboard marker, discussed their thinking, shared the work, and adjusted as needed.

The teacher circulated, giving hints and directions but not answers (using a different marker colour) and only answered questions strategically so that the answers moved the learning forward. As learners were successful in completing the first problem, the teacher offered them another, increasingly complex SolveMe mobile task. As the lesson progressed, knowledge and understanding were mobilized and shared throughout the room and across groups, as learners collaborated, supported one another, and built autonomy, naturally mixing and sharing ideas. This provided all learners the opportunity to participate in a non-threatening way, as they made their way through the succession of low-floor, high-ceiling problem-solving tasks.

The class later came together to consolidate their thinking and debrief, often having groups share their process and thinking aloud for the benefit of all class members. At the end of the class, learners were given independent time to reflect, take notes, and document some of their personal learning from the lesson in their math journal.

---

Dimensions of Global Competencies in Action

Communication

• Learners express ideas and emotions while following context cues (e.g., text features, non-verbal communication, tone of voice, digital images or icons) and conventions.
• Learners thoughtfully consider audience, purpose, context, modes, and forms to effectively share ideas.
• Learners seek to understand others’ messages through observation, active listening, and questioning.
• Learners make connections and build relationships through conversations and discussions both in person and in digital contexts.
• Learners value how communication strengthens community.

Collaboration

• Learners welcome and seek to understand diverse perspectives, voices, and ideas.
• Learners understand that building on others’ ideas deepens thinking.
• Learners value and put trust in others’ contributions.
• Learners practise active listening and asking questions of themselves and others.
• Learners work through differences and show a willingness to compromise or change perspective when appropriate.
• Learners co-construct meaning with others.
• Learners contribute equitably to the collective purpose or common goal.