Le programme d’études de mathématiques de la maternelle à la 12e année du programme d’immersion française est conçu pour répondre aux intérêts, habiletés et besoins des élèves, leur permettant ainsi de réaliser que les mathématiques représentent un moyen de construire leur compréhension du monde et qu’elles font partie de leur vie quotidienne.
Les résultats d'apprentissage de ce programme d’études sont répartis en quatre domaines :
Ces domaines reflètent nature des mathématiques de la maternelle à la 12e année.
L’étude des mathématiques favorise le développement des compétences globales et sous-tend les apprentissages durables. Elle favorise également le développement de la pensée logique et de compétences en résolution de problèmes et en analyse de données.
Les situations d'apprentissage et d’évaluation qui se déroulent en classe de mathématiques découlent d'une approche centrée sur l’apprentissage par la résolution de problèmes qui permet aux élèves de faire des liens entre leur compréhension conceptuelle et les divers processus mathématiques. L’intégration de ces processus lors des apprentissages amène les élèves à comprendre la nature des mathématiques et à leur donner un sens afin qu'ils puissent les apprendre et les utiliser à l'école et à l’extérieur de l’école tout au long de leur vie.
L’apprentissage en mathématiques tient compte du rôle du programme d’immersion française, de sa vision, de ses fondements (langue, culture et identité) ainsi que des principes de l’apprentissage et de l’évaluation. Les élèves de mathématiques sont exposés à la fois à des modèles mathématiques et à des modèles culturels et langagiers.
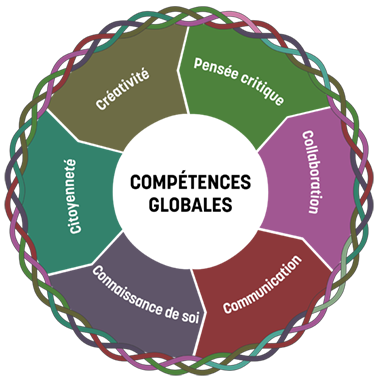

La pensée critique en mathématiques comprend la capacité de comparer, des représentations, des plans ou des solutions en utilisant des arguments logiques, des critères et des preuves. Elle requiert une métacognition chez les élèves leur permettant de résoudre des de communiquer leur raisonnement de façon efficace et de prendre des décisions éthiques.

La pensée créative en mathématiques comprend l’adoption d’un mode de pensée flexible, la curiosité, la prise de risques et l’établissement de liens avec les connaissances antérieures chez les élèves afin d’arriver à des solutions novatrices à divers problèmes et situations mathématiques en les envisageant sous un nouvel angle ou en formulant de nouvelles hypothèses.

La citoyenneté en mathématiques comprend le développement d’une littératie mathématique permettant l’application d’idées et de concepts mathématiques dans divers contextes de la vie quotidienne, éveillant ainsi la curiosité des élèves en ce qui concerne leur rôle de citoyens capables de contribuer activement à la société, de réfléchir de manière critique sur le monde, de prendre des décisions éclairées et de générer des solutions à un enjeu en tenant compte de diverses perspectives.

La connaissance de soi en mathématiques comprend la croyance des élèves en leur capacité à aborder et accomplir des tâches, à résoudre des problèmes et des situations mathématiques et à persévérer devant les défis auxquels ils font face en mathématiques. Elle comprend aussi la capacité des élèves à s’engager de façon positive dans des pratiques réflexives sur leurs apprentissages afin de se fixer des buts pour s’améliorer.

La collaboration en mathématiques comprend l’adhérence à une culture d’échanges d’idées et de points de vue chez les élèves afin de s’améliorer à la fois collectivement et individuellement et d’apprendre des autres et avec les autres pour développer et appliquer de nouvelles idées en mathématiques.

La communication en mathématiques comprend la capacité des élèves à échanger leurs idées, leur raisonnement et leurs solutions mathématiques de diverses façons notamment, de façon orale, écrite, concrète, imagée et symbolique dans divers contextes. Elle permet aux élèves de clarifier et de valider leurs idées et leur raisonnement, ainsi que de remettre en question leurs attitudes et leurs croyances à l’égard des mathématiques.
Les mathématiques, un outil à cultiver
Le développement de connaissances et d’habiletés en mathématiques permet de comprendre notamment des démarches, des théorèmes, des concepts, des situations et leur application. Cette construction d’un savoir mathématique permet de se définir comme étant des citoyens qui croient en leur capacité à réaliser une tâche, un apprentissage, un défi avec succès, les motivant ainsi à s’engager dans l’action et à persévérer tout au long de leur vie pour atteindre leur objectif.
Les mathématiques, un outil pour voir les choses autrement
Les mathématiques sont vivantes, elles développent la capacité de penser de manière fluide et créative, de comprendre, d’interpréter et de représenter de façon logique divers phénomènes parfois imperceptibles ou abstraits, de les mettre en perspectives les uns par rapport aux autres et de les analyser sous un œil différent.
Les mathématiques, un outil indispensable pour comprendre le monde
Les mathématiques contribuent à l’analyse, à la compréhension, à l’interprétation et à la description du monde dans lequel nous vivons. Elles permettent notamment d’étudier des quantités, des ordres, des espaces, des nombres et des figures et les liens qui existent entre ceux-ci.
Les mathématiques, un outil transversal indispensable pour l’avancement de la société
Les mathématiques occupent une place importante dans notre quête d’innovations et de solutions aux divers enjeux auxquels nous faisons face dans l’avancement de notre société. Elles sont utilisées en lien avec d’autres disciplines pour comprendre, décrire et interpréter les phénomènes qui nous entourent et elles permettent aux chercheurs d’améliorer nos conditions de vie en innovant et développant de nouvelles technologies.
Les mathématiques, un outil indispensable dans tous les aspects de la vie quotidienne
Les mathématiques sont omniprésentes dans la société. Elles nous permettent de nous doter de connaissances et d’habiletés nécessaires pour analyser l’information dans divers contextes sociaux, personnels, économiques, politiques, culturels et environnementaux de façon critique afin de faire des choix et de prendre des décisions éclairées, éthiques et durables dans tous les aspects de la vie quotidienne.